The alignment of nucleic acid or protein sequences constitutes an important step in many bioinformatics methods. Dayhoff matrices are part of a theoretically sound method for scoring biological sequence alignments. This bio-recipe shows how to compute Dayhoff matrices from mutation matrices and vice versa.
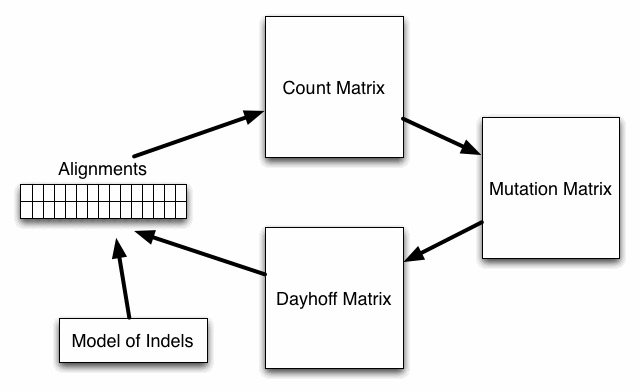
The way in which Dayhoff matrices are computed is outlined in the above figure. First pairs of aligned amino acids in verified alignments are used to build a count matrix, then the count matrix is used to estimate a mutation matrix at 1 PAM (evolutionary unit). From the mutation matrix, a Dayhoff scoring matrix is constructed. This Dayhoff matrix along with a model of indel events is then used to score new alignments which can then be used in an iterative process to construct new count matrices. This process is continued until convergence.
Alignments
Alignments can be computed exactly using dynamic programming methods (e.g. Needleman-Wunsch algorithm for global alignments) that compute alignments maximizing a scoring function. All alignment algorithms require a scoring matrix in which each element is the score of aligning one character (amino acids for the case of proteins) with another. One sensible way of scoring a particular alignment is to compare the probability that the sequences are aligned by reasons of common ancestry with the probability that the alignment arose by chance. To compute this probability, we need a model of evolution. A Markovian model of evolution will be used to compute the probability that the alignment arose by reasons of common ancestry while the product of the database frequencies of the aligned amino acids will be used as the probability of alignment by chance.
Markovian model of evolution
The Markovian model of evolution is a simple yet powerful and widely accepted model of evolution. The following assumptions are inherent in the use of a Markovian model:
| - | Neighbor Independence - Each symbol mutates randomly and independently of each other, i.e. the mutation of one amino acid is completely uncoupled from that of its neighbors. |
| - | Positional Independence - The probability of mutating from amino acid i (Ai) to amino acid j (Aj) depends only on Ai and Aj. A mutation from T to S in one part of the sequence has the same probability of occurence as a mutation from T to S in another part of the sequence. |
| - | History Independence - A Markovian model is memoryless. The probability of mutation at each site only depends on the present state (and not on its history). |
This model is, of course, an approximation. Real proteins adopt three-dimensional conformations where amino acids distant in the sequence come in contact and therefore interact. Thus, residues in a protein sequence need not undergo substitutions independent of substitutions at other positions in the protein. Likewise, biological function constrains the types of amino acid substitutions that are acceptable at difference positions. Therefore, amino acids need not suffer mutation independently, either in sequence or in time. It is well known that amino acids near an active site are more conserved than expected under the Markov model. Back mutations are also more probable than the corresponding mutation. For example if we have a F -> G -> F mutation, the G -> F mutation is more probable than a random G-> F mutation because we know that at one point in time the F was already accepted by natural selection (the protein was working with the F in the first place so mutating back to F has a high probability of not killing the organism). Protein evolution is not Markovian but as is often the case in biology, nature is too complex for us to model exactly. Therefore we use a Markovian model of evolution.
The Markovian model of mutation is usually combined with a model for insertion deletion events.
Initial Alignments
In the bio-recipe "Unbiased selection of sample alignments", we show how to compute an unbiased set of alignments between closely related sequences (PAM distance 40 to 80) from the SwissProt database. We shall use that set of alignments to count mutations between pairs of AA, paving the way to the scoring matrix.
If you want to try out this bio-recipe, you have to download SwissProt.Z and SampleAls.drw and change the pathnames in the following code to fit your system.
CreateDayMatrices(); SwissProt := '/home/darwin/Repositories/teaching/bio-recipes/Dayhoff/SwissProt.Z': ReadDb(SwissProt); CreateDayMatrices();
Reading 169638448 characters from file /home/darwin/Repositories/teaching/bio-recipes/Dayhoff/SwissProt.Z Pre-processing input (peptides) 163235 sequences within 163235 entries considered Peptide file(/home/darwin/Repositories/teaching/bio-recipes/Dayhoff/SwissProt.Z( 169638448), 163235 entries, 59631787 aminoacids)
Wait a minute! These sequences were aligned using the Dayhoff matrices, the very scoring matrices we strive for! Actually, if we didn't have alignments, we would start with alignments computed using a very basic scoring function, say, the identity matrix, count the mutations, compute a new, better scoring function and iterate until convergence. When working with closely related sequences, the process converges in just a few steps. Here, we are going to do only one step and start from the alignments obtained in the aforementioned bio-recipe:
ReadProgram( '/home/darwin/Repositories/teaching/bio-recipes/Dayhoff/SampleAls.drw' ); length(SampleAl);
333
Computing the Count matrix
First we construct the count matrix by looping through all alignments and counting matches and mismatches in a 20x20 matrix. The matches are tallied as a 1 in the appropriate diagonal matrix element. For a mismatch between Ai and Aj, we don't know which amino acid mutated into which, so we count 1/2 in element ij and 1/2 in element ji.
CountMatrix := CreateArray(1..20,1..20,0):
for i to length(SampleAl) do
# we use the DynProgStrings function as handle
s1 := DynProgStrings(SampleAl[i])[2]:
s2 := DynProgStrings(SampleAl[i])[3]:
for j to length(s1) do
# we convert the one letter code to integers
k1 := AToInt(s1[j]); k2 := AToInt(s2[j]);
# if k = 0, we have most likely a gap, if k = 21, we
# have an missing AA in the sequence (an "X")
if k1 > 0 and k1 < 21 and k2 > 0 and k2 < 21 then
if k1 = k2 then
CountMatrix[k1,k2] := CountMatrix[k1,k2] + 1;
else
CountMatrix[k1,k2] := CountMatrix[k1,k2] + 1/2;
CountMatrix[k2,k1] := CountMatrix[k2,k1] + 1/2;
fi
fi
od
od:
print(CountMatrix);
4372 121 113 162 96 140 324 387 40 136 212 219 72 50 213 596 300 6 39 428
121 2748 100 70 20 188 170 88 69 48 85 679 38 26 46 129 110 10 30 59
113 100 1727 322 16 92 166 190 89 37 42 209 17 18 38 207 160 4 40 45
162 70 322 3092 8 127 732 154 68 18 36 176 11 14 67 204 120 4 24 28
96 20 16 8 680 6 6 20 6 30 30 12 10 22 6 61 54 7 16 83
140 188 92 127 6 1367 346 58 70 35 100 310 52 18 48 128 103 6 30 66
324 170 166 732 6 346 3378 138 63 40 68 411 29 13 93 212 192 6 28 104
387 88 190 154 20 58 138 5788 30 19 36 136 14 17 46 230 78 8 12 40
40 69 89 68 6 70 63 30 1059 14 39 92 16 54 34 48 40 13 96 27
136 48 37 18 30 35 40 19 14 3217 858 72 198 144 24 55 156 12 37 1300
212 85 42 36 30 100 68 36 39 858 5061 124 410 331 62 104 133 20 92 593
219 679 209 176 12 310 411 136 92 72 124 3054 48 23 84 216 172 4 32 84
72 38 17 11 10 52 29 14 16 198 410 48 923 82 12 38 64 5 24 134
50 26 18 14 22 18 13 17 54 144 331 23 82 2191 14 38 39 59 367 101
213 46 38 67 6 48 93 46 34 24 62 84 12 14 2757 147 66 2 10 54
596 129 207 204 61 128 212 230 48 55 104 216 38 38 147 2326 490 13 28 100
300 110 160 120 54 103 192 78 40 156 133 172 64 39 66 490 2808 4 31 299
6 10 4 4 7 6 6 8 13 12 20 4 5 59 2 13 4 582 48 14
39 30 40 24 16 30 28 12 96 37 92 32 24 367 10 28 31 48 1612 42
428 59 45 28 83 66 104 40 27 1300 593 84 134 101 54 100 299 14 42 3784
Computing a 1-PAM mutation matrix
The transition probabilities between amino acids are described by a 20x20 mutation matrix which describes a particular evolutionary distance and is denoted by M with
M[j,i] = Pr{AA i -> AA j}
We are now going to compute a mutation matrix describing an amount of evolution in which, on average, 1% of the AA in a given sequence changes. This matrix is also known as the 1-PAM (for "Point Accepted Mutations", an accepted mutation being a mutation that survives in the population) mutation matrix. We want to compute the transition probabilities for each AA. So far, we have counted the number of transitions in our sample. We must now normalize each column so that their sum is equal to 1:
N := CreateArray(1..20,1..20,0): for i to 20 do N[i,i] := 1/sum(CountMatrix[i]): od: MutationMatrix := CountMatrix*N: print(MutationMatrix);
0.54 0.03 0.03 0.03 0.08 0.04 0.05 0.05 0.02 0.02 0.03 0.04 0.03 0.01 0.06 0.11 0.06 0.01 0.01 0.06 0.02 0.57 0.03 0.01 0.02 0.06 0.03 0.01 0.04 0.01 0.01 0.11 0.02 0.01 0.01 0.02 0.02 0.01 0.01 0.01 0.01 0.02 0.48 0.06 0.01 0.03 0.03 0.03 0.05 0.01 0.01 0.03 0.01 0.00 0.01 0.04 0.03 0.00 0.02 0.01 0.02 0.01 0.09 0.57 0.01 0.04 0.11 0.02 0.03 0.00 0.00 0.03 0.01 0.00 0.02 0.04 0.02 0.00 0.01 0.00 0.01 0.00 0.00 0.00 0.57 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.01 0.00 0.01 0.01 0.01 0.01 0.01 0.02 0.04 0.03 0.02 0.01 0.42 0.05 0.01 0.04 0.01 0.01 0.05 0.02 0.00 0.01 0.02 0.02 0.01 0.01 0.01 0.04 0.04 0.05 0.13 0.01 0.11 0.52 0.02 0.03 0.01 0.01 0.07 0.01 0.00 0.02 0.04 0.04 0.01 0.01 0.01 0.05 0.02 0.05 0.03 0.02 0.02 0.02 0.77 0.02 0.00 0.00 0.02 0.01 0.00 0.01 0.04 0.01 0.01 0.00 0.01 0.01 0.01 0.02 0.01 0.01 0.02 0.01 0.00 0.54 0.00 0.00 0.01 0.01 0.02 0.01 0.01 0.01 0.02 0.04 0.00 0.02 0.01 0.01 0.00 0.03 0.01 0.01 0.00 0.01 0.50 0.10 0.01 0.09 0.04 0.01 0.01 0.03 0.02 0.01 0.18 0.03 0.02 0.01 0.01 0.03 0.03 0.01 0.00 0.02 0.13 0.60 0.02 0.19 0.09 0.02 0.02 0.02 0.02 0.03 0.08 0.03 0.14 0.06 0.03 0.01 0.09 0.06 0.02 0.05 0.01 0.01 0.50 0.02 0.01 0.02 0.04 0.03 0.01 0.01 0.01 0.01 0.01 0.00 0.00 0.01 0.02 0.00 0.00 0.01 0.03 0.05 0.01 0.42 0.02 0.00 0.01 0.01 0.01 0.01 0.02 0.01 0.01 0.00 0.00 0.02 0.01 0.00 0.00 0.03 0.02 0.04 0.00 0.04 0.61 0.00 0.01 0.01 0.07 0.14 0.01 0.03 0.01 0.01 0.01 0.00 0.01 0.01 0.01 0.02 0.00 0.01 0.01 0.01 0.00 0.72 0.03 0.01 0.00 0.00 0.01 0.07 0.03 0.06 0.04 0.05 0.04 0.03 0.03 0.02 0.01 0.01 0.04 0.02 0.01 0.04 0.43 0.09 0.02 0.01 0.01 0.04 0.02 0.04 0.02 0.04 0.03 0.03 0.01 0.02 0.02 0.02 0.03 0.03 0.01 0.02 0.09 0.52 0.01 0.01 0.04 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.02 0.00 0.00 0.00 0.71 0.02 0.00 0.00 0.01 0.01 0.00 0.01 0.01 0.00 0.00 0.05 0.01 0.01 0.01 0.01 0.10 0.00 0.01 0.01 0.06 0.61 0.01 0.05 0.01 0.01 0.01 0.07 0.02 0.02 0.01 0.01 0.20 0.07 0.01 0.06 0.03 0.01 0.02 0.06 0.02 0.02 0.51
The mutation matrix describes the mutations observed in our sample. Let us compute the average percentage of AA mutation, that is, average change. To do this, we first need to compute the AA frequencies.
Freq := CreateArray(1..20,0): Tot := sum(sum(CountMatrix)): for i to 20 do Freq[i] := sum(CountMatrix[i])/Tot: od: print(Freq);
[0.08477395, 0.05103334, 0.03837665, 0.05740129, 0.01256165, 0.03471746, 0.06883297, 0.07907659, 0.02077239, 0.06813598, 0.08906677, 0.06501537, 0.02318017, 0.03823936, 0.04036729, 0.05668318, 0.05721648, 0.00871765, 0.02785317, 0.07797831]
PercentageMutation := 100 * sum(Freq[i] * (1 - MutationMatrix[i,i]),i=1..20);
PercentageMutation := 44.5302
Remember that we want to calculate the 1-PAM matrix. From the definition, we know that the percentage of mutations and the PAM distance coincide at a PAM distance of 1. As the PAM distance increases, there is a departure between the two: the percentage of mutations incrases more slowly. This is intuitive in that the probability of a mutation reoccuring at a given site increases with an increasing amount of mutations. In addition, there is a certain probability that amino acids will mutate back to their original state. The formal relationship between our matrix and the 1-PAM matrix is the following:
k MutationMatrix = PAM1
Hence
(1/k) PAM1 = MutationMatrix
Or
ln(MutationMatrix)
ln(PAM1) = ------------------
k
We can solve this formula numerically using an iterative process where k - that is the PAM distance - is approximated at each step by the percentage of mutations.
PAM1 := MutationMatrix:
lnPAM1 := ln(MutationMatrix):
k := 1:
RateMutation := sum(Freq[i] * (1 - PAM1[i,i]), i= 1..20):
iter := 0:
# The following loop goes until the difference reach the computer's
# precision.
while abs(RateMutation - 0.01) > DBL_EPSILON do
iter := iter + 1;
k:= k * RateMutation * 100:
lnPAM1 := lnPAM1 / (RateMutation * 100):
PAM1 := exp(lnPAM1):
RateMutation := sum(Freq[i] * (1 - PAM1[i,i]), i= 1..20);
printf('After %d iteration(s), k=%f, RateMutation=%f
', iter, k, RateMutation);
od:
After 1 iteration(s), k=44.530219, RateMutation=0.014324 After 2 iteration(s), k=63.785069, RateMutation=0.010027 After 3 iteration(s), k=63.959878, RateMutation=0.010000 After 4 iteration(s), k=63.960985, RateMutation=0.010000 After 5 iteration(s), k=63.960992, RateMutation=0.010000 After 6 iteration(s), k=63.960992, RateMutation=0.010000 After 7 iteration(s), k=63.960992, RateMutation=0.010000 After 8 iteration(s), k=63.960992, RateMutation=0.010000
Here are the 10 first rows and columns of the PAM1 matrix
PrintMatrix(transpose(transpose(PAM1[1..10])[1..10]),'% .5f ');
0.99002 0.00040 0.00048 0.00048 0.00193 0.00090 0.00115 0.00112 0.00031 0.00018 0.00024 0.99072 0.00052 0.00013 0.00035 0.00140 0.00045 0.00019 0.00075 0.00011 0.00022 0.00039 0.98805 0.00162 0.00028 0.00065 0.00046 0.00057 0.00121 0.00011 0.00033 0.00015 0.00242 0.99064 0.00006 0.00071 0.00311 0.00036 0.00071 0.00002 0.00029 0.00009 0.00009 0.00001 0.99123 0.00001 -0.00001 0.00004 0.00005 0.00006 0.00037 0.00095 0.00059 0.00043 0.00003 0.98585 0.00157 0.00011 0.00095 0.00004 0.00094 0.00060 0.00083 0.00373 -0.00005 0.00312 0.98900 0.00029 0.00057 0.00004 0.00104 0.00030 0.00117 0.00050 0.00027 0.00026 0.00034 0.99589 0.00024 0.00002 0.00008 0.00031 0.00065 0.00026 0.00008 0.00057 0.00017 0.00006 0.99023 0.00001 0.00015 0.00014 0.00019 0.00003 0.00032 0.00008 0.00004 0.00002 0.00005 0.98765
We observe that the PAM value k of our original matrix is 63.9610, which is rather good news, knowing that we constructed it using alignments of distance 40 to 80 PAM.
But the presence of negative transition probabilities in our 1-PAM matrix is rather disturbing. Obviously, our dataset has trouble fitting to the Markovian model. To some extent, the Markovian model has some limitations, but mainly, our sample is too small: looking back at our count matrix, we see that the negative probabilities correspond to cases with very few counts. It turns out that taking larger samples generally solves the negative values problem. In our case, we are going to replace the negative non-diagonal elements in the log matrix with 0 and remove the difference from the diagonal so that the sum of all probabilities for each AA still adds to 0.
for i to 20 do
for j to 20 do
if lnPAM1[i,j] < 0 and j <> i then
diff:= 0 - lnPAM1[i,j];
lnPAM1[i,j] := lnPAM1[i,j] + diff;
lnPAM1[j,j] := lnPAM1[j,j] - diff;
fi:
od:
od:
PAM1 := exp(lnPAM1):
PrintMatrix(transpose(transpose(PAM1[1..10])[1..10]),'% .5f ');
0.99002 0.00040 0.00048 0.00048 0.00193 0.00090 0.00115 0.00112 0.00031 0.00018 0.00024 0.99072 0.00052 0.00013 0.00035 0.00140 0.00045 0.00019 0.00075 0.00011 0.00022 0.00039 0.98805 0.00162 0.00028 0.00065 0.00046 0.00057 0.00121 0.00011 0.00033 0.00015 0.00242 0.99064 0.00006 0.00071 0.00311 0.00036 0.00071 0.00002 0.00029 0.00009 0.00009 0.00001 0.99118 0.00001 0.00000 0.00004 0.00005 0.00006 0.00037 0.00095 0.00059 0.00043 0.00003 0.98585 0.00157 0.00011 0.00095 0.00004 0.00094 0.00060 0.00083 0.00373 0.00000 0.00312 0.98899 0.00029 0.00057 0.00004 0.00104 0.00030 0.00117 0.00050 0.00027 0.00026 0.00034 0.99589 0.00024 0.00002 0.00008 0.00031 0.00065 0.00026 0.00008 0.00057 0.00017 0.00006 0.99023 0.00001 0.00015 0.00014 0.00019 0.00003 0.00032 0.00008 0.00004 0.00002 0.00005 0.98765
To compute n-PAM matrices, we multiply the PAM1 matrix through itself N times, which is most efficiently achieved through n additions in log space.
Computing Dayhoff matrices from PAM mutation matrices and AA frequency
In the introduction, we motivated the quest for mutation matrices through the need of a method to quantify the evolutionary relationship of two AA. We now have such matrices. Remember that we are interested in the ratio
P("alignment i and j arose through evolution")
----------------------------------------------
P("alignment i and j arose by chance")
Let us now assume that the sequences of i and j have a PAM distance of 250. The probability that i and j and have evolved from a common ancestor is the following:
-----
\
Numerator = ) f[x] Pr(x -> i) Pr(x -> j)
/
-----
x
-----
\ 125 125
Numerator = ) f[x] (M )[i, x] (M )[j, x]
/
-----
x
We know from the construction of the mutation matrices that
k k f[i] (M )[j, i] = f[j] (M )[i, j]
Hence
-----
\ 125 125
Numerator = ) (M )[i, x] f[x] (M )[j, x]
/
-----
x
-----
\ 125 125
Numerator = ) (M )[i, x] f[j] (M )[x, j]
/
-----
x
250 Numerator = f[j](M )[i, j]
250 Numerator = f[i](M )[j, i]
Knowing that the probability that the alignments i and j arose by chance is the product of the frequencies, our ratio is now:
250
P("alignment i and j arose through evolution") f[i](M )[j, i]
---------------------------------------------- = ----------------
P("alignment i and j arose by chance") f[i] f[j]
We can now compute the alignment that maximizes the product of these ratios for each position in the alignment, through dynamic programming for instance. To speed up the process, we can maximize the sum of the logs. And to speed it up even more, we can precompute and store the values of all pairs of AA, therefore computing the *Dayhoff Matrix* (in honor of Margaret O. Dayhoff, who computed them first). The exact value of each cell of the 250-PAM Dayhoff Matrix is:
250
(M )[i, j]
D[ij] = 10 log[10](------------)
f[i]
So let us now compute the Dayhoff Matrix for a PAM distance of 250:
PAM250 := exp(250*lnPAM1):
Dayhoff250 := CreateArray(1..20,1..20):
for i to 20 do
for j to 20 do
Dayhoff250[i,j] := 10*log10(PAM250[i,j]/Freq[i]);
od:
od:
print(Dayhoff250);
2.7 -0.9 -0.4 -0.4 1.0 -0.2 -0.0 0.4 -1.3 -1.1 -1.3 -0.5 -1.0 -2.5 0.6 1.2 0.5 -3.4 -2.6 -0.2 -0.9 5.0 0.4 -0.4 -1.4 1.6 0.5 -1.5 0.7 -2.8 -2.3 3.0 -1.5 -2.9 -1.4 -0.1 -0.4 -2.4 -2.0 -2.5 -0.4 0.4 3.8 2.2 -1.0 0.7 1.0 0.6 1.3 -3.1 -3.0 0.9 -2.3 -2.9 -1.1 0.8 0.4 -3.1 -1.4 -2.6 -0.4 -0.4 2.2 4.8 -2.4 1.0 2.9 -0.4 0.4 -4.5 -4.1 0.6 -3.3 -4.4 -0.8 0.5 -0.3 -4.3 -2.9 -3.6 1.0 -1.4 -1.0 -2.4 9.8 -1.7 -2.1 -1.8 -1.5 0.1 -0.7 -1.8 -0.5 -0.2 -2.2 0.7 0.8 0.7 -0.2 1.0 -0.2 1.6 0.7 1.0 -1.7 3.0 1.7 -1.5 0.9 -2.2 -1.7 1.7 -0.8 -2.5 -0.7 0.3 -0.0 -2.6 -1.6 -1.8 -0.0 0.5 1.0 2.9 -2.1 1.7 3.4 -1.0 0.1 -3.4 -3.2 1.2 -2.4 -4.1 -0.6 0.4 -0.1 -3.9 -2.9 -2.5 0.4 -1.5 0.6 -0.4 -1.8 -1.5 -1.0 7.0 -1.9 -5.4 -5.1 -1.1 -4.2 -5.4 -2.2 0.2 -1.7 -4.3 -4.8 -4.2 -1.3 0.7 1.3 0.4 -1.5 0.9 0.1 -1.9 7.1 -2.7 -1.8 0.6 -1.3 1.1 -0.6 -0.5 -0.7 1.4 3.0 -2.4 -1.1 -2.8 -3.1 -4.5 0.1 -2.2 -3.4 -5.4 -2.7 4.1 2.8 -2.7 2.3 0.8 -3.4 -2.2 -0.5 -1.4 -1.0 3.4 -1.3 -2.3 -3.0 -4.1 -0.7 -1.7 -3.2 -5.1 -1.8 2.8 4.0 -2.3 3.0 2.0 -2.7 -2.1 -1.1 -0.7 0.2 2.0 -0.5 3.0 0.9 0.6 -1.8 1.7 1.2 -1.1 0.6 -2.7 -2.3 3.2 -1.5 -3.3 -0.8 0.2 -0.1 -3.5 -2.3 -2.3 -1.0 -1.5 -2.3 -3.3 -0.5 -0.8 -2.4 -4.2 -1.3 2.3 3.0 -1.5 4.4 1.6 -2.7 -1.5 -0.6 -0.8 0.1 1.6 -2.5 -2.9 -2.9 -4.4 -0.2 -2.5 -4.1 -5.4 1.1 0.8 2.0 -3.3 1.6 7.1 -4.0 -2.7 -2.1 4.8 6.0 0.0 0.6 -1.4 -1.1 -0.8 -2.2 -0.7 -0.6 -2.2 -0.6 -3.4 -2.7 -0.8 -2.7 -4.0 8.6 0.5 -0.8 -5.1 -3.7 -2.4 1.2 -0.1 0.8 0.5 0.7 0.3 0.4 0.2 -0.5 -2.2 -2.1 0.2 -1.5 -2.7 0.5 2.3 1.5 -2.4 -2.3 -1.4 0.5 -0.4 0.4 -0.3 0.8 -0.0 -0.1 -1.7 -0.7 -0.5 -1.1 -0.1 -0.6 -2.1 -0.8 1.5 3.3 -3.2 -2.1 0.1 -3.4 -2.4 -3.1 -4.3 0.7 -2.6 -3.9 -4.3 1.4 -1.4 -0.7 -3.5 -0.8 4.8 -5.1 -2.4 -3.2 14.8 5.4 -1.8 -2.6 -2.0 -1.4 -2.9 -0.2 -1.6 -2.9 -4.8 3.0 -1.0 0.2 -2.3 0.1 6.0 -3.7 -2.3 -2.1 5.4 8.4 -1.5 -0.2 -2.5 -2.6 -3.6 1.0 -1.8 -2.5 -4.2 -2.4 3.4 2.0 -2.3 1.6 0.0 -2.4 -1.4 0.1 -1.8 -1.5 3.5
Computing the PAM mutation matrices and AA frequencies from the Dayhoff matrices
In some situations, we might like to reconstruct the mutation matrix and AA frequencies array from a Dayhoff matrix. Let us try to get the PAM250 mutation matrix from the corresponding Dayhoff matrix that we just calculated in the previous section. Remember the way we constructed the Dayhoff matrix:
M[i, j]
D[i, j] = 10 log[10](-------)
f[i]
Hence we have the following relationship:
M[i, j] (1/10 D[i, j] - 1/10 D[i, x]) ------- = 10 M[i, x]
For each row i, we can calculate the value of each cell i,j up to a scaling factor M[i,x]. Furthermore, we know that each column of the mutation matrix should sum up to 1. Combining these two facts, we can reconstitute the mutation matrix. So let us proceed step by step. For each row, we pose that sum(M[i,1], i=1..20) = 1 , and we compute the other cells from that result:
E := CreateArray(1..20,1..20):
for A to 20 do
for B to 20 do
E[B,A] := 10 ^ ((Dayhoff250[B,A]-Dayhoff250[B,1]) / 10)
od;
od:
print(E);
1.0 0.4 0.5 0.5 0.7 0.5 0.5 0.6 0.4 0.4 0.4 0.5 0.4 0.3 0.6 0.7 0.6 0.2 0.3 0.5 1.0 3.9 1.3 1.1 0.9 1.8 1.4 0.9 1.4 0.6 0.7 2.4 0.9 0.6 0.9 1.2 1.1 0.7 0.8 0.7 1.0 1.2 2.6 1.8 0.9 1.3 1.4 1.3 1.5 0.5 0.5 1.3 0.6 0.6 0.8 1.3 1.2 0.5 0.8 0.6 1.0 1.0 1.8 3.3 0.6 1.4 2.2 1.0 1.2 0.4 0.4 1.3 0.5 0.4 0.9 1.2 1.0 0.4 0.6 0.5 1.0 0.6 0.6 0.5 7.5 0.5 0.5 0.5 0.6 0.8 0.7 0.5 0.7 0.8 0.5 0.9 0.9 0.9 0.7 1.0 1.0 1.5 1.2 1.3 0.7 2.1 1.6 0.8 1.3 0.6 0.7 1.6 0.9 0.6 0.9 1.1 1.1 0.6 0.7 0.7 1.0 1.1 1.3 2.0 0.6 1.5 2.2 0.8 1.0 0.5 0.5 1.3 0.6 0.4 0.9 1.1 1.0 0.4 0.5 0.6 1.0 0.6 1.1 0.8 0.6 0.6 0.7 4.5 0.6 0.3 0.3 0.7 0.3 0.3 0.5 0.9 0.6 0.3 0.3 0.3 1.0 1.6 1.8 1.5 1.0 1.7 1.4 0.9 6.9 0.7 0.9 1.6 1.0 1.7 1.2 1.2 1.1 1.9 2.7 0.8 1.0 0.7 0.6 0.5 1.3 0.8 0.6 0.4 0.7 3.2 2.4 0.7 2.2 1.6 0.6 0.8 1.1 0.9 1.0 2.8 1.0 0.8 0.7 0.5 1.2 0.9 0.7 0.4 0.9 2.6 3.4 0.8 2.7 2.1 0.7 0.8 1.1 1.2 1.4 2.1 1.0 2.2 1.4 1.3 0.7 1.7 1.5 0.9 1.3 0.6 0.7 2.3 0.8 0.5 0.9 1.2 1.1 0.5 0.7 0.7 1.0 0.9 0.7 0.6 1.1 1.0 0.7 0.5 0.9 2.2 2.5 0.9 3.5 1.8 0.7 0.9 1.1 1.0 1.3 1.8 1.0 0.9 0.9 0.6 1.7 1.0 0.7 0.5 2.3 2.2 2.8 0.8 2.6 9.1 0.7 1.0 1.1 5.4 7.1 1.8 1.0 0.6 0.7 0.7 0.5 0.8 0.8 0.5 0.8 0.4 0.5 0.7 0.5 0.4 6.4 1.0 0.7 0.3 0.4 0.5 1.0 0.7 0.9 0.9 0.9 0.8 0.8 0.8 0.7 0.5 0.5 0.8 0.5 0.4 0.9 1.3 1.1 0.4 0.4 0.6 1.0 0.8 1.0 0.8 1.1 0.9 0.9 0.6 0.8 0.8 0.7 0.9 0.8 0.6 0.7 1.3 1.9 0.4 0.6 0.9 1.0 1.3 1.1 0.8 2.6 1.2 0.9 0.8 3.1 1.6 1.9 1.0 1.8 6.7 0.7 1.3 1.1 66.6 7.6 1.5 1.0 1.1 1.3 0.9 1.7 1.3 0.9 0.6 3.6 1.4 1.9 1.1 1.8 7.1 0.8 1.1 1.1 6.2 12.4 1.3 1.0 0.6 0.6 0.5 1.3 0.7 0.6 0.4 0.6 2.3 1.6 0.6 1.5 1.0 0.6 0.8 1.1 0.7 0.7 2.3
We now want to find for each row a scaling factor such that each column adds to 1. It is a system of 20 linear equations with 20 unknowns that can be easily solved through Gaussian elimination:
w := GaussElim(transpose(E),[seq(1,i=1..20)]);
w := [0.1563, 0.04162567, 0.03531554, 0.05183259, 0.01594234, 0.03277879, 0.06862222, 0.08690376, 0.01535841, 0.05327896, 0.06549119, 0.05848042, 0.01838480, 0.02142322, 0.04589026, 0.07465867, 0.06348041, 0.00395498, 0.01542346, 0.07489430]
Finally multiply each line by the appropriate weight:
for i to 20 do E[i] := E[i]*w[i] od: print(E);
0.16 0.07 0.08 0.08 0.11 0.08 0.08 0.09 0.06 0.07 0.06 0.08 0.07 0.05 0.10 0.11 0.09 0.04 0.05 0.08 0.04 0.16 0.06 0.05 0.04 0.07 0.06 0.04 0.06 0.03 0.03 0.10 0.04 0.03 0.04 0.05 0.05 0.03 0.03 0.03 0.04 0.04 0.09 0.06 0.03 0.04 0.05 0.04 0.05 0.02 0.02 0.05 0.02 0.02 0.03 0.05 0.04 0.02 0.03 0.02 0.05 0.05 0.10 0.17 0.03 0.07 0.11 0.05 0.06 0.02 0.02 0.07 0.03 0.02 0.05 0.06 0.05 0.02 0.03 0.03 0.02 0.01 0.01 0.01 0.12 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.02 0.01 0.01 0.02 0.03 0.05 0.04 0.04 0.02 0.07 0.05 0.02 0.04 0.02 0.02 0.05 0.03 0.02 0.03 0.04 0.03 0.02 0.02 0.02 0.07 0.08 0.09 0.13 0.04 0.10 0.15 0.05 0.07 0.03 0.03 0.09 0.04 0.03 0.06 0.07 0.07 0.03 0.04 0.04 0.09 0.06 0.09 0.07 0.05 0.06 0.06 0.39 0.05 0.02 0.02 0.06 0.03 0.02 0.05 0.08 0.05 0.03 0.03 0.03 0.02 0.02 0.03 0.02 0.01 0.03 0.02 0.01 0.11 0.01 0.01 0.02 0.02 0.03 0.02 0.02 0.02 0.03 0.04 0.01 0.05 0.04 0.03 0.02 0.07 0.04 0.03 0.02 0.04 0.17 0.13 0.04 0.12 0.08 0.03 0.04 0.06 0.05 0.05 0.15 0.07 0.05 0.04 0.03 0.08 0.06 0.04 0.03 0.06 0.17 0.22 0.05 0.18 0.14 0.05 0.05 0.07 0.08 0.09 0.14 0.06 0.13 0.08 0.07 0.04 0.10 0.09 0.05 0.08 0.04 0.04 0.14 0.05 0.03 0.05 0.07 0.06 0.03 0.04 0.04 0.02 0.02 0.01 0.01 0.02 0.02 0.01 0.01 0.02 0.04 0.05 0.02 0.06 0.03 0.01 0.02 0.02 0.02 0.02 0.03 0.02 0.02 0.02 0.01 0.04 0.02 0.01 0.01 0.05 0.05 0.06 0.02 0.06 0.20 0.02 0.02 0.02 0.12 0.15 0.04 0.05 0.03 0.03 0.03 0.02 0.03 0.04 0.02 0.04 0.02 0.02 0.03 0.02 0.02 0.29 0.05 0.03 0.01 0.02 0.02 0.07 0.06 0.07 0.06 0.07 0.06 0.06 0.06 0.05 0.03 0.03 0.06 0.04 0.03 0.06 0.10 0.08 0.03 0.03 0.04 0.06 0.05 0.06 0.05 0.07 0.06 0.06 0.04 0.05 0.05 0.04 0.06 0.05 0.04 0.05 0.08 0.12 0.03 0.04 0.06 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.01 0.01 0.01 0.00 0.01 0.03 0.00 0.01 0.00 0.26 0.03 0.01 0.02 0.02 0.02 0.01 0.03 0.02 0.01 0.01 0.06 0.02 0.03 0.02 0.03 0.11 0.01 0.02 0.02 0.10 0.19 0.02 0.07 0.04 0.04 0.03 0.10 0.05 0.04 0.03 0.04 0.17 0.12 0.05 0.11 0.08 0.04 0.06 0.08 0.05 0.06 0.18
Now see how well that compares to the matrix we started from in the last section:
print(PAM250);
0.16 0.07 0.08 0.08 0.11 0.08 0.08 0.09 0.06 0.07 0.06 0.08 0.07 0.05 0.10 0.11 0.09 0.04 0.05 0.08 0.04 0.16 0.06 0.05 0.04 0.07 0.06 0.04 0.06 0.03 0.03 0.10 0.04 0.03 0.04 0.05 0.05 0.03 0.03 0.03 0.04 0.04 0.09 0.06 0.03 0.04 0.05 0.04 0.05 0.02 0.02 0.05 0.02 0.02 0.03 0.05 0.04 0.02 0.03 0.02 0.05 0.05 0.10 0.17 0.03 0.07 0.11 0.05 0.06 0.02 0.02 0.07 0.03 0.02 0.05 0.06 0.05 0.02 0.03 0.03 0.02 0.01 0.01 0.01 0.12 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.02 0.01 0.01 0.02 0.03 0.05 0.04 0.04 0.02 0.07 0.05 0.02 0.04 0.02 0.02 0.05 0.03 0.02 0.03 0.04 0.03 0.02 0.02 0.02 0.07 0.08 0.09 0.13 0.04 0.10 0.15 0.05 0.07 0.03 0.03 0.09 0.04 0.03 0.06 0.07 0.07 0.03 0.04 0.04 0.09 0.06 0.09 0.07 0.05 0.06 0.06 0.39 0.05 0.02 0.02 0.06 0.03 0.02 0.05 0.08 0.05 0.03 0.03 0.03 0.02 0.02 0.03 0.02 0.01 0.03 0.02 0.01 0.11 0.01 0.01 0.02 0.02 0.03 0.02 0.02 0.02 0.03 0.04 0.01 0.05 0.04 0.03 0.02 0.07 0.04 0.03 0.02 0.04 0.17 0.13 0.04 0.12 0.08 0.03 0.04 0.06 0.05 0.05 0.15 0.07 0.05 0.04 0.03 0.08 0.06 0.04 0.03 0.06 0.17 0.22 0.05 0.18 0.14 0.05 0.05 0.07 0.08 0.09 0.14 0.06 0.13 0.08 0.07 0.04 0.10 0.09 0.05 0.08 0.04 0.04 0.14 0.05 0.03 0.05 0.07 0.06 0.03 0.04 0.04 0.02 0.02 0.01 0.01 0.02 0.02 0.01 0.01 0.02 0.04 0.05 0.02 0.06 0.03 0.01 0.02 0.02 0.02 0.02 0.03 0.02 0.02 0.02 0.01 0.04 0.02 0.01 0.01 0.05 0.05 0.06 0.02 0.06 0.20 0.02 0.02 0.02 0.12 0.15 0.04 0.05 0.03 0.03 0.03 0.02 0.03 0.04 0.02 0.04 0.02 0.02 0.03 0.02 0.02 0.29 0.05 0.03 0.01 0.02 0.02 0.07 0.06 0.07 0.06 0.07 0.06 0.06 0.06 0.05 0.03 0.03 0.06 0.04 0.03 0.06 0.10 0.08 0.03 0.03 0.04 0.06 0.05 0.06 0.05 0.07 0.06 0.06 0.04 0.05 0.05 0.04 0.06 0.05 0.04 0.05 0.08 0.12 0.03 0.04 0.06 0.00 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.01 0.01 0.01 0.00 0.01 0.03 0.00 0.01 0.00 0.26 0.03 0.01 0.02 0.02 0.02 0.01 0.03 0.02 0.01 0.01 0.06 0.02 0.03 0.02 0.03 0.11 0.01 0.02 0.02 0.10 0.19 0.02 0.07 0.04 0.04 0.03 0.10 0.05 0.04 0.03 0.04 0.17 0.12 0.05 0.11 0.08 0.04 0.06 0.08 0.05 0.06 0.18
Finally, we would like to calculate the AA frequencies from the mutation matrix. What do we know about it? We know that
F[i] M[i, j] = F[j] M[j, i]
The other constraint, clearly, is that all frequencies sum up to 1. Hence, we can proceed in the same fashion as above, calculating all frequencies using, say, F[1]=1, then scale the frequencies so that they add to 1:
f:= [seq( E[i,1]/E[1,i], i=1..20 )]: f:= f/sum(f): print(f);
[0.08477395, 0.05103334, 0.03837665, 0.05740129, 0.01256165, 0.03471746, 0.06883297, 0.07907659, 0.02077239, 0.06813598, 0.08906677, 0.06501537, 0.02318017, 0.03823936, 0.04036729, 0.05668318, 0.05721648, 0.00871765, 0.02785317, 0.07797831]
which perfectly matches our original frequency array:
print(Freq);
[0.08477395, 0.05103334, 0.03837665, 0.05740129, 0.01256165, 0.03471746, 0.06883297, 0.07907659, 0.02077239, 0.06813598, 0.08906677, 0.06501537, 0.02318017, 0.03823936, 0.04036729, 0.05668318, 0.05721648, 0.00871765, 0.02785317, 0.07797831]
Written by Christophe Dessimoz and Gina Gannarozzi, based to a large extent on material from Darwin 1.6 Tutorial as well as personal notes from Gaston Gonnet for the last part. Revision and suggestions by Adrian Schneider.
© 2011 by CBRG Group, Informatik, ETH Zurich
Last updated on Thu Oct 6 11:24:33 2011 by zo
!!! This document is stored in the ETH Web archive and is no longer maintained !!!